2024-11-08
King Salmonid Probability Curve
Splatoon 3 has Salmon Run. Salmon Run has King Salmonid. BUT! You don't get it every time.
We all know that the chance of a King Salmonid spawning is related to your Salmometer.
What's the relation though?
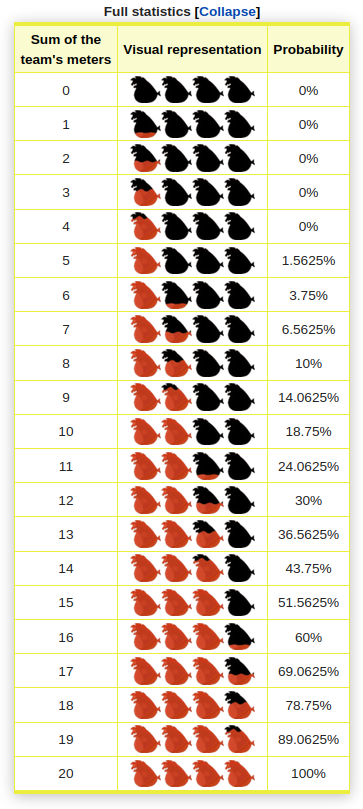
Well, on [Inkipedia's Salmometer page](https://splatoonwiki.org/wiki/King_Salmonid#Salmometer) they have a lookup table for the probability,
which is just copied from [Leanny's website](https://leanny.github.io/splat3/coop.html).
|But I don't like lookup tables.|
In fact, I just don't like remembering a lot of things.
I know you aren't supposed to recite this, but it would save me a lot of time when I'm explaining to people if I don't have to look it up.
(Plus, I'm a computer science student and math nerd.)
So I set off to a journey (on stream) to find a single function that maps to all these probability.
It wasn't that hard.
The steps I took can be traced pretty easily.
- Map each Salmometer level and their corresponding probability into |x and y coordinates|. (0 ≤ x ≤ 20, 0 ≤ y ≤ 1)
- |Express all y coordinates in fractions| instead of decimals.
- Find the |common denominator| of these probabilities, which is `320`.
At this point, I realized numerator of each subsequent probability after `x = 4` is just the previous numerator increased by 5, 7, 9, etc.
I concluded that the probability of each level is just a |sum of arithmetic series|, where the said arithmetic series is basically |5, 7, 9, ...|
While it took me a bit to recall the formula for summation of arithmetic series, it was pretty much smooth sailing at this point.
After finding out the formula, we just put that as the numerator, which is `(2(x - 5) + 5 + 5) \* (x - 4) / 2`.
If you want an explanation of that, the second `(x - 4)` is the amount of terms we have since `x = 4`.
`5` is the first term, and `2(x - 5) + 5` is the last term at `x`.
By simplifying this, you'll get the equation `y = (x \^ 2 - 4x) / 320`.
(Obviously, probabilities below 0 doesn't exist. We'll just clamp that to 0, and so does the game.)
And this is much better!
Instead of remembering 21 lines of the table, |now I only need 1 equation!|
Sure, it is a bit harder to obtain the value, but in terms of time complexity this is still |O(1)|, so this is great!